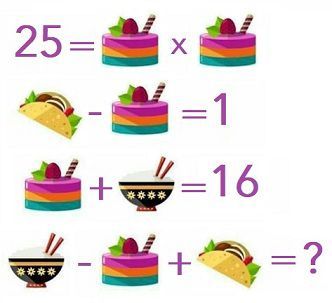Introduction
Les mathématiques sont souvent perçues comme une discipline austère, réservée aux seuls passionnés ou aux étudiants en sciences. Cependant, elles sont omniprésentes dans notre quotidien, que ce soit dans la gestion de nos finances, la planification de nos voyages ou même la cuisine. L’un des aspects les plus intéressants des mathématiques est sans doute la résolution d’énigmes. Ces défis ludiques nous invitent à réfléchir de manière créative et à appliquer nos connaissances mathématiques d’une manière amusante. Dans cet article, nous explorons l’importance des mathématiques, les différents types d’énigmes, et nous résoudrons une énigme particulière ensemble.
I. L’Importance des Mathématiques dans la Vie Quotidienne
A. Un outil essentiel
Les mathématiques sont fondamentales dans de nombreux domaines. Que ce soit pour gérer son budget, mesurer des distances, ou même évaluer des probabilités, les mathématiques nous permettent de prendre des décisions éclairées. Par exemple, lorsque nous faisons des cours, nous comparons souvent les prix au kilo pour choisir le meilleur rapport qualité-prix. Cela nécessite des compétences de calcul simples, mais essentielles.
B. Développement de la Pensée Critique
Les mathématiques nous enseignent à penser de manière critique et logique. Elles nous aident à analyser des situations, à établir des connexions entre des concepts et à résoudre des problèmes complexes. Ces compétences sont transférables à d’autres domaines, comme la science, l’économie, ou même les arts. En développant notre pensée critique à travers les mathématiques, nous devenons des décideurs plus compétents et plus efficaces.
II. Les Types d’Énigmes Mathématiques
A. Énigmes Arithmétiques
Les énigmes arithmétiques impliquent des opérations de base comme l’addition, la soustraction, la multiplication et la division. Elles sont souvent conçues pour tester notre capacité à manipuler des chiffres et à résoudre des problèmes simples. Prenons l’exemple suivant :
Énigme :
25 = (Gâteau) × x – (Taco) = 1
(Gâteau) + (Riz) = 16
(Taco) – (Riz) + (Taco) = ?
B. Énigmes Logiques
Les énigmes logiques nécessitent une réflexion plus approfondie et impliquent souvent des relations entre différents éléments. Elles peuvent inclure des puzzles, des séquences ou des problèmes de déduction. Ces types d’énigmes sont souvent plus complexes et demandent une attention particulière aux détails.
C. Énigmes Géométriques
Ces énigmes impliquent des formes, des angles et des surfaces. Elles peuvent inclure des calculs d’aire, de périmètre ou de volume. Les énigmes géométriques sont souvent utilisées pour enseigner des concepts fondamentaux en géométrie.
III. Résolution de l’Énigme
Revenons à notre énigme initiale. Pour résoudre ce type de problème, nous devons d’abord attribuer une valeur à chaque symbole. Commençons par identifier les variables :
- Gâteau = G
- Taco = T
- Riz = R
Nous avons donc les équations suivantes :
- 25=G×x−T=125 = G \times x – T = 1
- G+R=16G + R = 16
- T−R+T=?T – R + T = ?
A. Résolution des Équations
- Première Équation :
G×x−T=1G \times x – T = 1
Cela signifie que G×x=T+1G \times x = T + 1. - Deuxième Équation :
G+R=16G + R = 16
Nous pouvons exprimer RR comme R=16−GR = 16 – G. - Troisième Équation :
T−R+T=2T−RT – R + T = 2T – R
Nous devons trouver RR en fonction de GG pour substituer dans cette équation.